Introduction
字节Seed团队和清华合作提出了DAPO,一种全开源的,基于PPO的强化学习方法,一用于提升LLM的reasoning能力。
Preliminary
Preliminary包括PPO,GRPO还有KL divergence
PPO
PPO的训练目标为:
$$ \mathcal{J}_{\mathrm{PPO}}(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},o_{\leq t}\sim \pi_{\theta_{old}}(\cdot\mid q)}\left[ \min\left(r_t(\theta)\hat{A}_t,\mathrm{clip}\left(r_t(\theta), 1-\epsilon, 1+\epsilon\right)\hat{A}_t\right) \right] $$其中
$$ r_t(\theta) = \frac{\pi_{\theta}(o_t\mid q, o_{< t})}{\pi_{\theta_{old}}(o_t\mid q, o_{< t})} $$$(q,a)$ 是从数据集 $\mathcal{D}$ 采样的QA pair,$\epsilon>0$ 是一个超参数,$\hat{A}_t$ 是 $t$时刻的优势估计 (advantage estimator). 给定 value function $V$ 以及 reward function $R$, $\hat{A}_t$ 通过计算GAE得到:
$$ \hat{A}_t^{\mathrm{GAE}(\gamma, \lambda)}=\sum_{k=0}^{\infty}(\gamma\lambda)^k\delta_{t+k} $$其中
$$ \delta_k = R_k + \gamma V(s_{k+1})-V(s_k),\quad 0\leq \gamma,\lambda\leq 1 $$GRPO
相比于PPO,GRPO不依赖于value function, 因此不需要使用reward model. GRPO通过一组输出来估计value $V(s)$, 然后进行更新。具体来说,给定 QA pair $(q,a)$, 我们从$\pi_{\theta_{old}}$中采样$G$个输出 ${o_i}{i=1}^G$, 接下来我们基于reward ${R_i}{i=1}^G$ 使用如下表达式来估计group-level reward:
$$ \hat{A}_{i,t} = \frac{r_i - \mathrm{mean}(\{R_i\}_{i=1}^G)}{\mathrm{std}(\{R_i\}_{i=1}^G)} $$最后,GRPO的训练目标与PPO类似,只不过将 $\hat{A}t$ 替换为 $\hat{A}{i,t}$, 然后在分组上进行了归一化:
$$ \mathcal{J}_{\mathrm{GRPO}}(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},\{o_i\}_{i=1}^G\sim \pi_{\theta_{old}}(\cdot\mid q)}\left[ \frac{1}{G}\sum_{i=1}^G\frac{1}{|o_i|}\sum_{t=1}^{|o_i|}\min\left(r_{i,t}(\theta)\hat{A}_{i,t},\mathrm{clip}\left(r_{i,t}(\theta), 1-\epsilon, 1+\epsilon\right)\hat{A}_{i,t}\right) \right] $$其中,
$$ r_{i,t}(\theta) = \frac{\pi_{\theta}(o_{i,t}\mid q, o_{i,< t})}{\pi_{\theta_{old}}(o_{i,t}\mid q, o_{i,< t})} $$KL divergence
在传统的RLHF框架中,我们再PPO的基础上,增加了一个KL divergence正则项,用于约束新旧策略的差异。具体来说,给定旧策略 $\pi_{\theta_{old}}$ 和新策略 $\pi_{\theta}$,我们实际上优化的损失函数为
$$ \mathcal{J}_{\mathrm{RLHF}}(\theta) = \mathcal{J}_{\mathrm{PPO}}(\theta) - \beta\mathrm{KL}\left(\pi_{\theta_{old}}(\cdot\mid q)\|\pi_{\theta}(\cdot\mid q)\right) $$其中,$\beta$ 是一个超参数,用于平衡PPO损失和KL divergence损失。上面的PPO损失函数也可以改为GRPO损失函数。
作者在本文中认为,reasoning model和RLHF的训练目标是不一样的,RLHF加上KL divergence正则项,会使得模型在推理时过于保守,偏向于explotition而reasoning model则需要exploration。因此,作者在本文中去掉了这一项。
Rule-based reward modeling
作者基于final accuracy来作为outcome reward, 避免模型训练出现reward hacking问题。reward function 如下:
$$ R(\hat{y},y) = \begin{cases} 1, & \text{if is\_equivalent}(\hat{y},y) \\ -1, & \text{otherwise} \end{cases} $$DAPO
DAPO基于GRPO改进,其优化的目标函数为:
$$ \mathcal{J}_{\mathrm{DAPO}}(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},\{o_i\}_{i=1}^G\sim \pi_{\theta_{old}}(\cdot\mid q)}\left[ \frac{1}{\sum_{t=1}^G|o_i|}\sum_{i=1}^G\sum_{t=1}^{|o_i|}\min\left(r_{i,t}(\theta)\hat{A}_{i,t},\mathrm{clip}\left(r_{i,t}(\theta), 1-\epsilon_{low}, 1+\epsilon_{high}\right)\hat{A}_{i,t}\right) \right] s.t. \quad 0< \vert \{o_i\mid \text{is\_equivalent}(o_i,a)\} \vert < G $$其中,$\alpha$ 是一个超参数,用于约束输出数量, $r_{i,t}(\theta)$ 和 $\hat{A}_{i,t}$ 的定义与GRPO相同。
接下来就是DAPO算法的几个关键点:
Clip-Higher
作者认为,PPO和GRPO存在entropy collapse问题,也就是policy的entropy会迅速的下降,导致最终每个group的输出基本都差不多,模型很难探索到新的知识。因此,作者提出了Clip-Higher策略,也就是说,让模型能够充分探索。
作者举了一个例子,当 $\epsilon=0.2$ 时,如果一个group的输出为 $[0.01, 0.9]$, 那么在clip之后,最大的更新幅度为 $[0.01, 0.9]\times 0.2=[0.002, 0.18]$. 这对于概率比较小的输出来说,很难帮助模型提升。因此,作者修改了其阈值。进一步地,作者分离了clip的阈值,分别使用 $\epsilon_{low}$ 和 $\epsilon_{high}$ 来约束更新幅度。作者通过实验验证了这个例子,结果如下图所示:
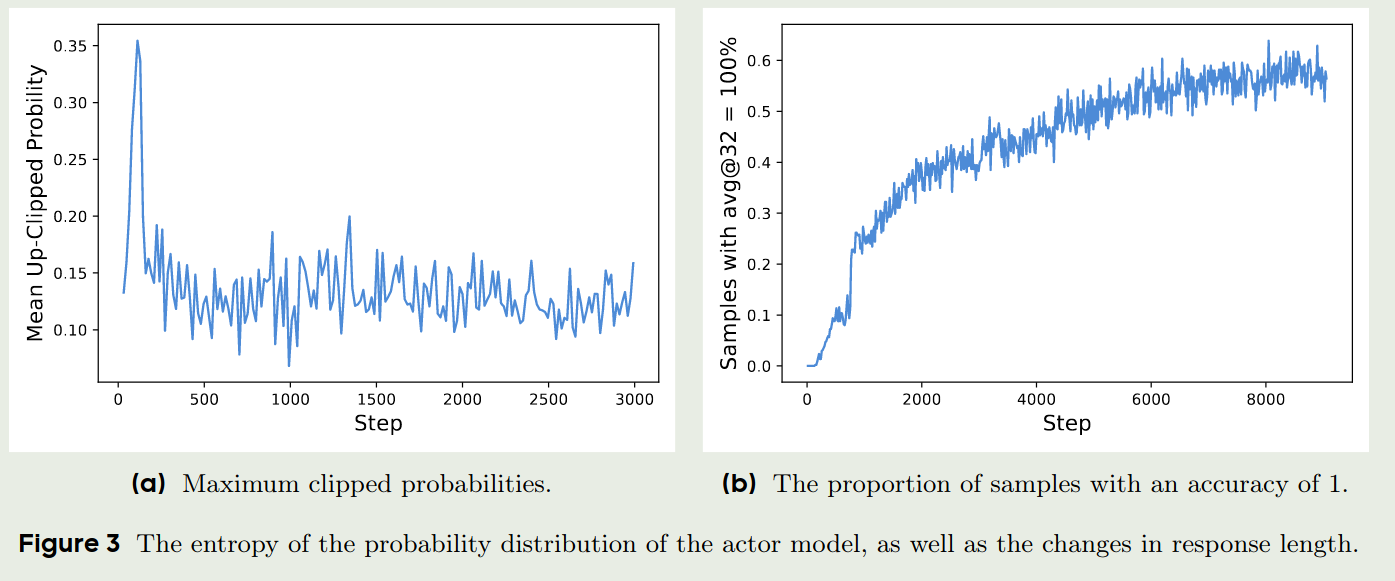
最后,加入Clip-Higher策略的DAPO的训练目标为,与GRPO的训练目标相比,我们使用 $\epsilon_{low}$ 和 $\epsilon_{high}$ 来约束更新幅度。
$$ \mathcal{J}_{\mathrm{DAPO}}(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},\{o_i\}_{i=1}^G\sim \pi_{\theta_{old}}(\cdot\mid q)}\left[ \frac{1}{\sum_{t=1}^G|o_i|}\sum_{i=1}^G\sum_{t=1}^{|o_i|}\min\left(r_{i,t}(\theta)\hat{A}_{i,t},\mathrm{clip}\left(r_{i,t}(\theta), 1-\epsilon_{low}, 1+\epsilon_{high}\right)\hat{A}_{i,t}\right) \right] s.t. \quad 0< \vert \{o_i\mid \text{is\_equivalent}(o_i,a)\} \vert < G $$在实际训练中,作者使用了一个比较大的 $\epsilon_{high}$ 来保证概率较小的token也能有较大的概率被采样到。 Clip-Higher的实验结果如下图所示:
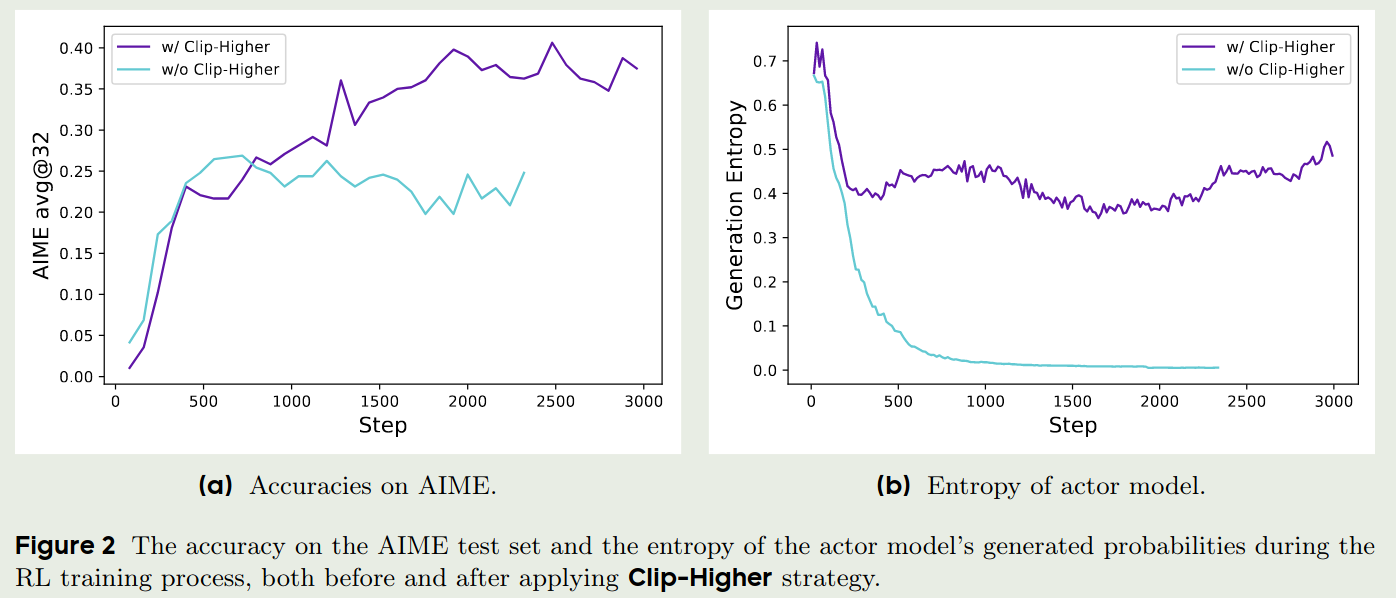
Dynamic Sampling
作者认为,在GRPO中,如果一个group的输出全都是对的,那么其advantage会趋近于0,结果导致 policy 不会得到更新,这样就降低了采样效率。
为了解决这个问题,坐着提出了over-sample以及filtering策略,来过滤accracy等于1或者0的prompts,也就是DAPO中的约束项:
$$ s.t. \quad 0< \vert \{o_i\mid \text{is\_equivalent}(o_i,a)\} \vert < G $$通过增加这个约束项,我们可以保证每个group的输出不会趋同,从保证模型能够得到更新,以提高采样效率。实验结果如下图所示:
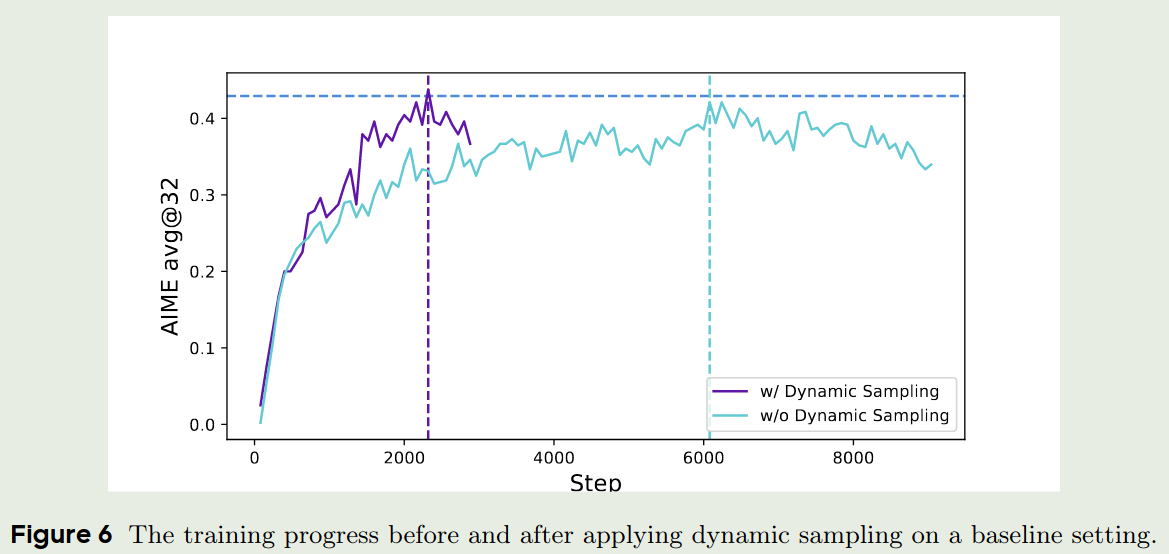
Token-level policy gradient loss
GRPO采用了一个sample-level的loss计算方式,也就是GRPO首先在每个sample中计算每个token的损失并进行平均,然后在不同的sample中在此进行平均。在这种方式下,每个sample对最终的loss贡献是相同的。这样就导致两个问题:
- 对于高质量的long answer,通过在token层面进行平均,因为answe比较长,因此整体loss会比较低,也就会降低这个sample的贡献,导致模型很难学习到长答案。
- 一些非常长的sample,其往往包含gibberish或者repetitive tokens,这些sample对模型训练是有害的
因此,为了解决这个问题,作者提出了Token-level policy gradient loss,也就是我们改变了求和方式
$$ \frac{1}{G}\sum_{i=1}^G\frac{1}{|o_i|}\sum_{t=1}^{|o_i|}\left(\cdot\right)\to \frac{1}{\sum_{t=1}^G|o_i|}\sum_{i=1}^G\sum_{t=1}^{|o_i|}\left(\cdot\right) $$通过这种方式,我们让长回答的loss贡献更大,从而提高模型学习长回答的能力。另一方面,现在每个token对整体loss的贡献是相同的,一些关键token的loss也会被放大,从而提高模型的表现。
实验结果如下图所示:
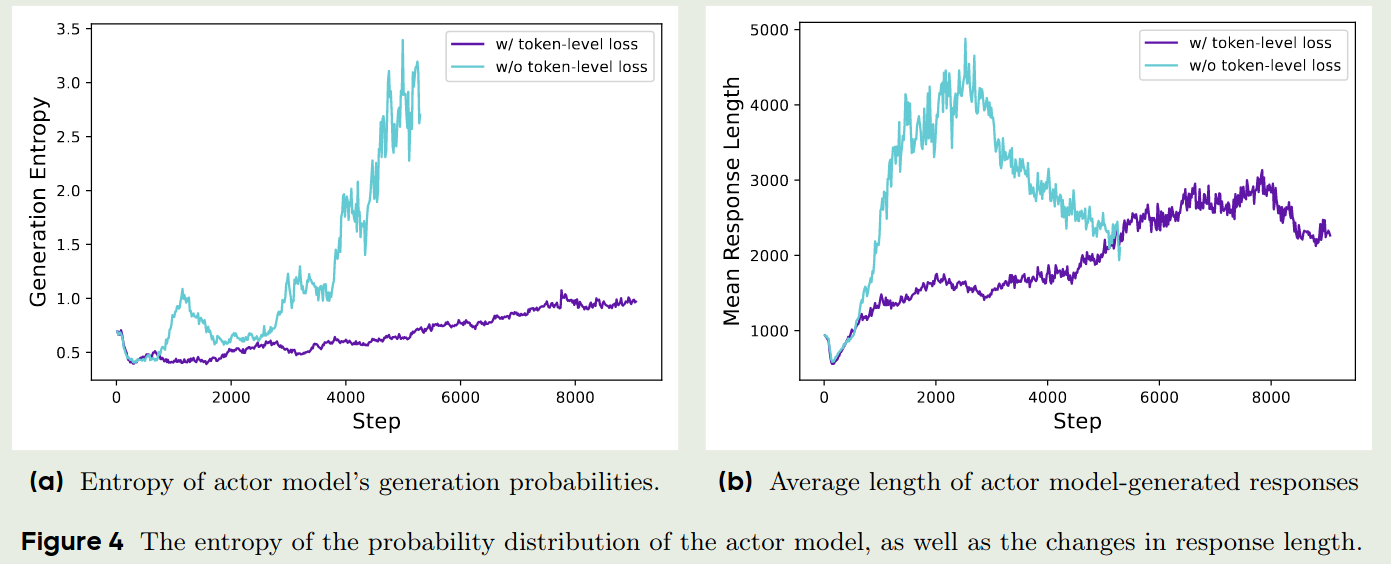
Overlong reward shaping
与Kimi-k1.5类似,DAPO也增加了length penalty,用于惩罚过长的回答。作者首先使用了一个overlong filtering技巧,来mask掉truncated samples的loss,作者发现通过这个技巧,可以提升模型的训练稳定性以及表现,实验结果如下图所示
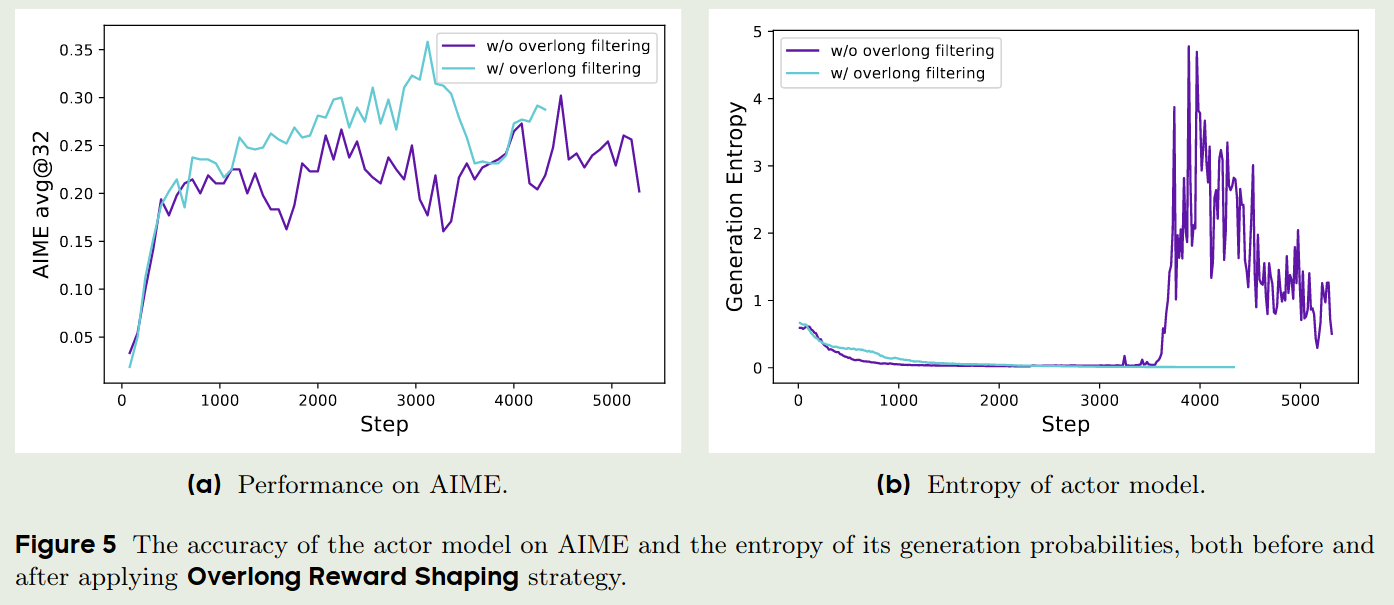
作者还提出了soft overlong punishment, 用于reshape truncated samples的reward,表达式如下:
$$ R_{length}(y) = \begin{cases} 0, & \text{if } |y|\leq L_{\max}-L_{cache} \\ \frac{(L_{\max}-L_{cache})-|y|}{L_{cache}}, & \text{if } L_{\max}-L_{cache}<|y|\leq L_{\max} \\ -1, & \text{if } |y|>L_{\max} \end{cases} $$算法
DAPO的算法流程如下:

实验
数据集
作者构建了DAPO-Math-17K数据集用于DAPO的训练,该数据集从AoPS得到,包含了17K prompts,每个prompt都对应一个整数作为答案。
训练细节
作者以GRPO作为baseline, $G=16$, $L_{\max}=16384$, $L_{cache}=4096$, $\epsilon_{low}=0.2$, $\epsilon_{high}=0.28$
评估时,使用AIME作为benchmark,以 avg@32作为指标,temperature设置为1.0, topp设置为0.7。
实验结果
DAPO与GRPO的对比如下图所示:
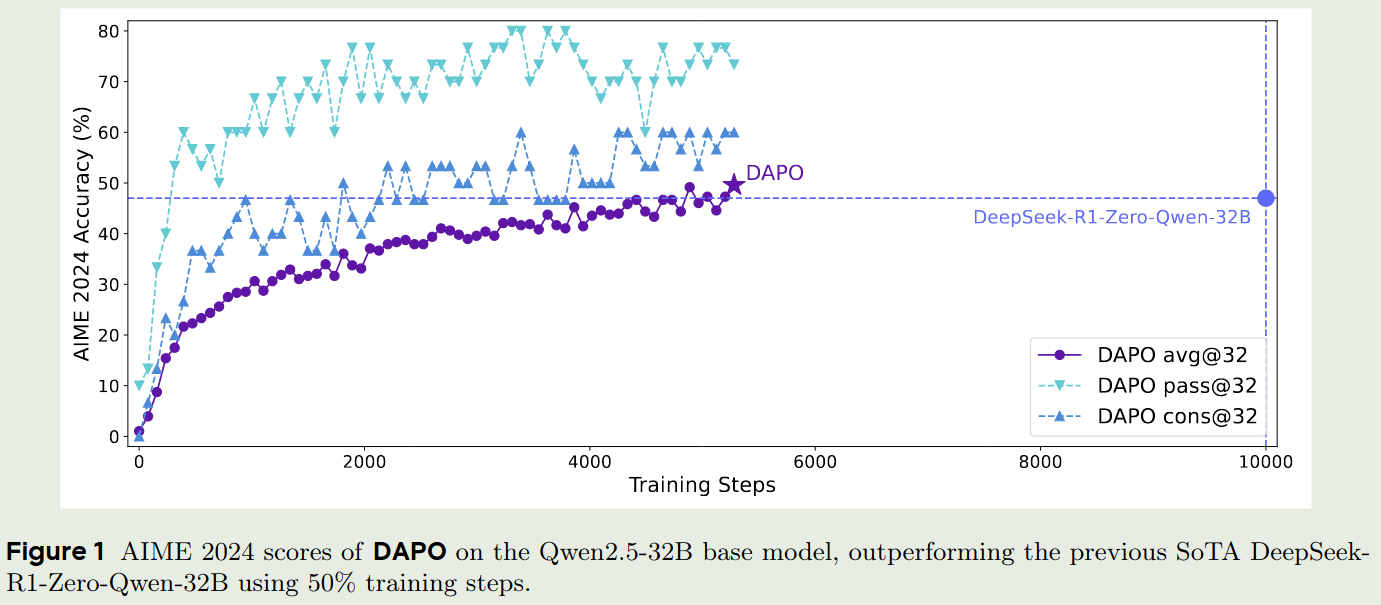
Ablation study
作者探究了每一个部分对最终表现的影响,结果如下:
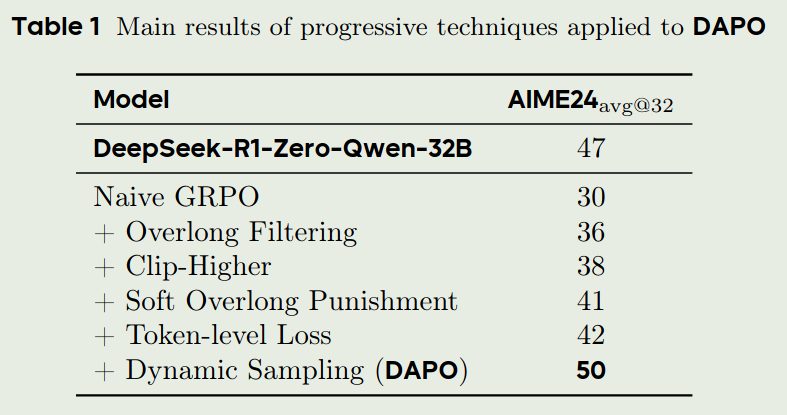
traing dynamics
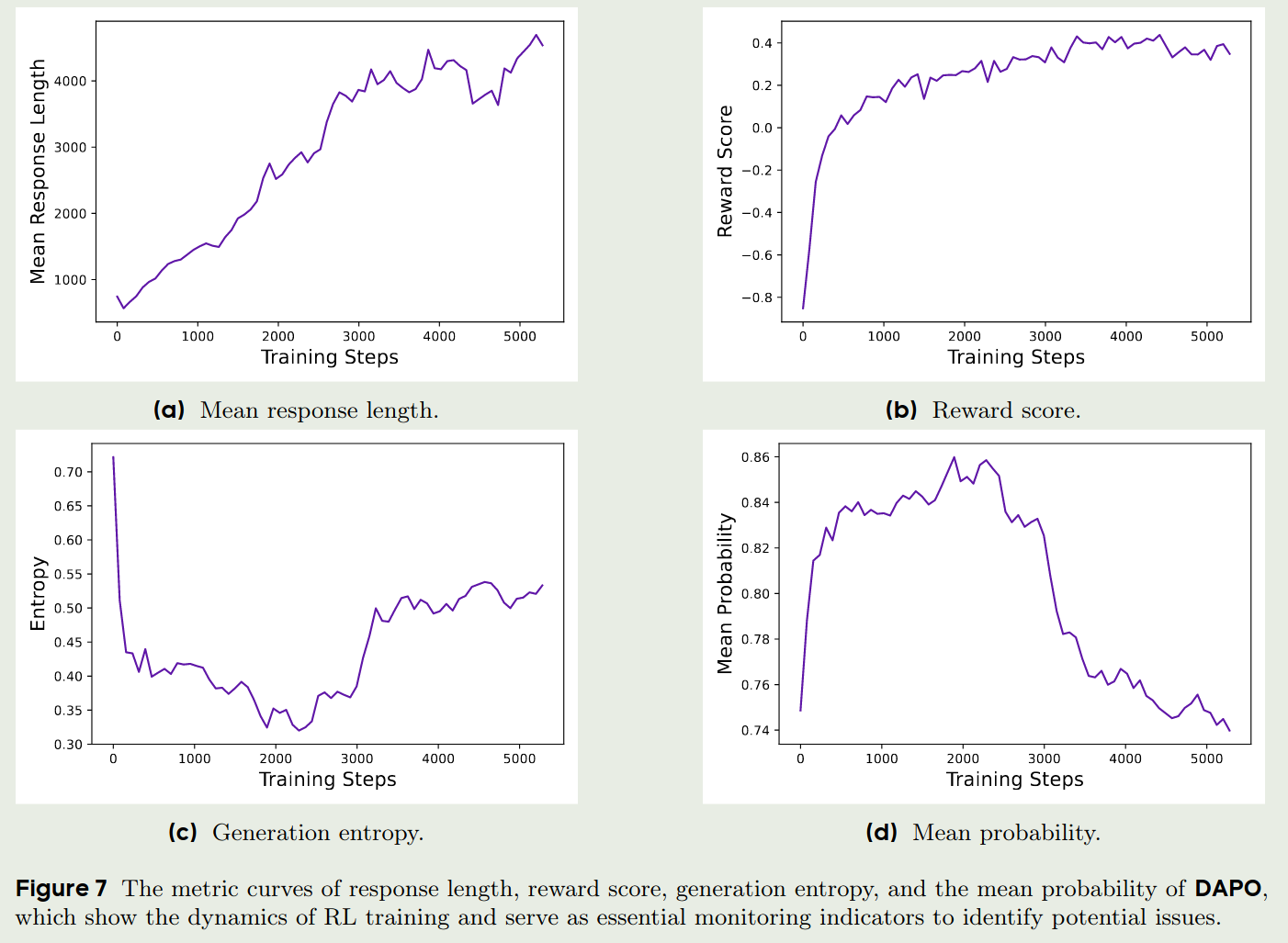
作者还探究了mean response length, reward score, generation entropy以及mean probability随训练轮数的变化,其中:
- mean response length: 在一定程度上反应了模型训练的稳定性和表现
- reward score: 反应模型的表现,作者认为,给定一个reliable reward signal, LLM可以很好的fit到训练数据集上,但是作者发现最终的reward与val score相关性比较大,很可能是因为模型过拟合了
- generation entropy & mean probability: 代表了模型的探索能力,通过实验结果可以看到,DAPO初期的探索能力比较强,但是随着训练的进行,探索能力下降,利用能力增强。
结果如下:
结论
作者基于GRPO提出了DAPO,一种全开源的,基于PPO的强化学习方法,用于提升LLM的reasoning能力。作者首先分析了GRPO损失函数存在的不足,然后进行了针对性改进,包括Clip-Higher, Dynamic Sampling, Token-level policy gradient loss以及Overlong reward shaping。作者通过实验验证了DAPO的有效性,并探究了DAPO的训练动态。